Présentation du programme d'étude
de la radioactivité et de la décroissance exponentielle.
Simulation numérique.
Menu général

* Il y a 6 possibilités de simulation ;
1- Etude de l'évolution d'une population de
noyaux radioactifs sur un réseau.
2- Etude de la décroissance exponentielle,
avec un jeu de dés.
3- Etude de la répartition des nombres de désintégrations
pendant une durée déterminée, cas du Césium 137
4- Etude de l'influence de la distance source compteur.
5- Etude de l'absorption du rayonnement par l'aluminium.
6- Etude de l'absorption du rayonnement par le plomb.
* En cas de bloquage du programme, ou si les valeurs des variables entrées imposent un temps de calcul trop
long, il est toujours possible de stopper le programme par la séquence habituelle de touches clavier "Ctrl
"+"Alt"+Suppr". Il faut alors relancer l'application.
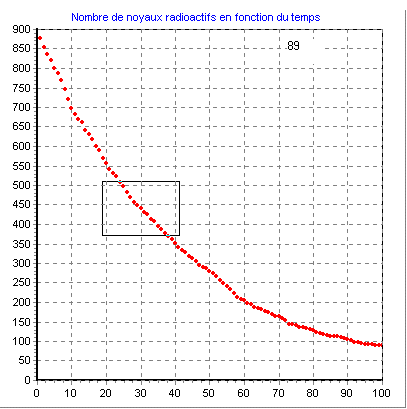
Evolution de la population des noyaux radioactifs sur un réseau :

Variables :
* Atome, permet d'avoir une décroissance de la population de noyaux radioactifs correspondants aux noyaux
choisis, à partir du paramètre lambda.
* Unité de temps, doit être adaptée noyaux choisis.
* Taille du réseau, les valeurs utilisables dépendent des performances de la machine utilisée.
* Durée, fixe la durée d'observation en unité de temps.
* Le tracé peut être linéaire ou logarithmique
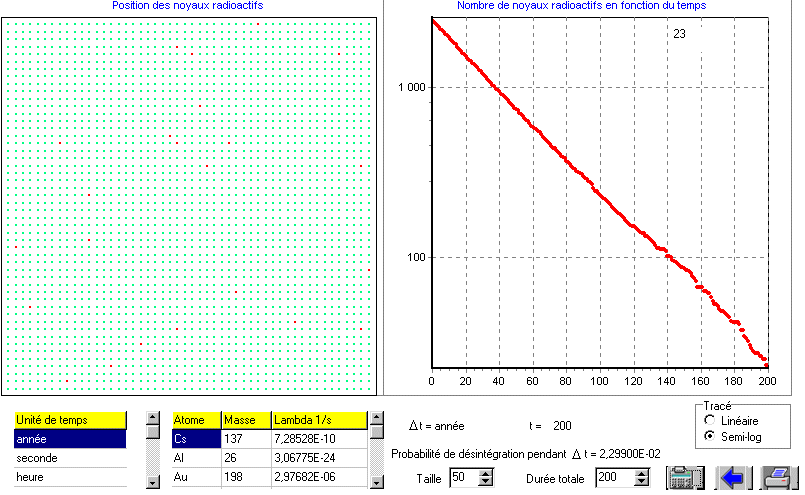
On peut choisir un nouvel atome en descendant l'ascenceur du tableau Atome jusqu'a la dernière case qui
peut être éditée.
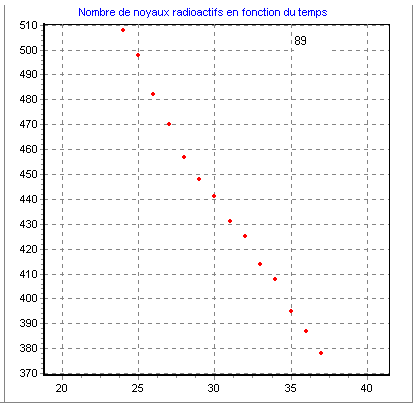
Dans le cas d'un choix de l'unité mal adaptée, on peut avoir :
|
trop court |
trop long |
Etude de la décroissance exponentielle,
avec un jeu de dés.
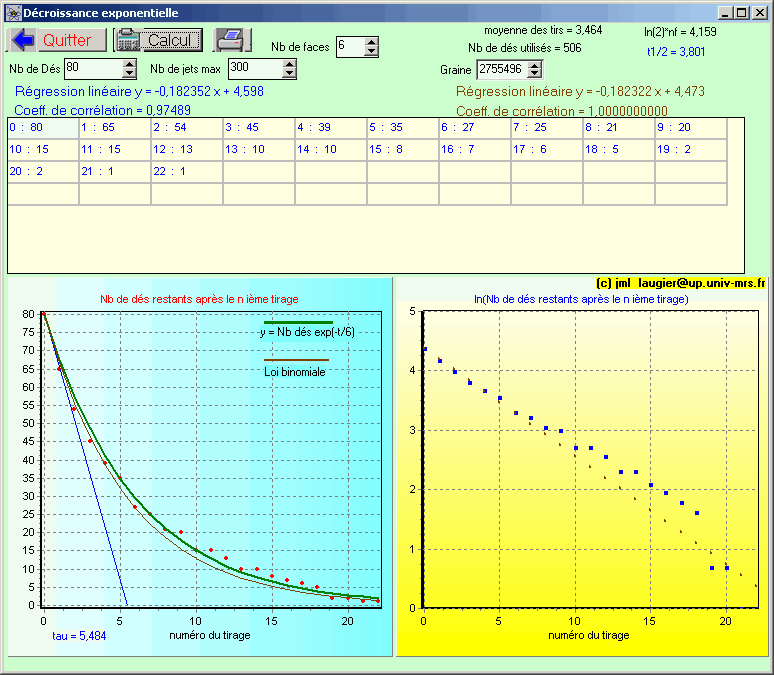
Le programme permet de choisir :
* le nombre de dés.
* le nombre de jets successifs.
* le nombre de faces du dé (de 2à 500).
* la graine du générateur de nombres aléatoires
On obtient trois courbes, expérimentale (numérique), la loi théorique du type N0 exp(-t/nb
de faces), la loi binomiale.

Etude de l'activité avec le nombre de désintégrations mesuré
pendant 'Durée de comptage' et avec 'Nb de mesures'
Le programme affiche :
* moyenne N et écart-type expérimental.
* l'écart-type théorique égal à la racine carrée de la moyenne.
* l'histogramme des mesures.
* les points correspondant à une distribution de Poisson théorique de moyenne N et d'écart-type
EctTh (théorique)
* les points correspondant à une distribution de Gauss théorique de moyenne N et d'écart-type
EcartType (expérimental)
Suivant les choix proposés on peut obtenir :
Une distribution de Poisson ou une distribution qui peut être approchée par une Gaussienne (figure
précédente)
Signification de l'histogramme :
Dans le cas expérimental suivant;
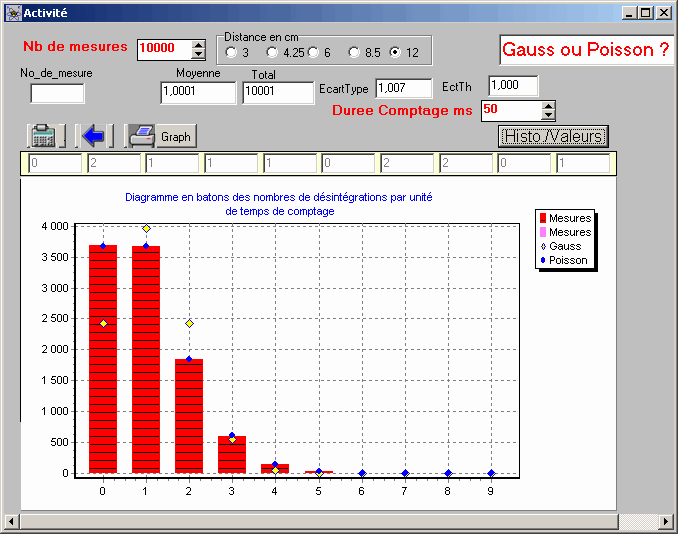
on a obtenu les valeurs suivantes
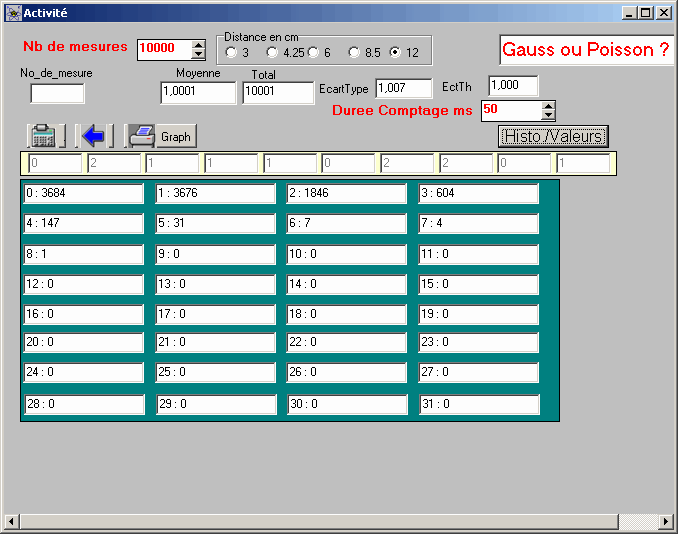
c'est à dire :
3684 fois 0 désintégration pendant 50ms,
3676 fois 1 désintégration pendant 50ms,
1846 fois 2 désintégrations pendant 50ms,
604 fois 3 désintégrations pendant 50ms,
147 fois 4 désintégrations pendant 50ms,
31 fois 5 désintégrations pendant 50ms,
7 fois 6 désintégrations pendant 50ms.....
4 fois 7désintégrations pendant 50ms,
1 fois 8désintégrations pendant 50ms...
0 fois 32 ou plus de désintégrations pendant 50ms,
Dans le cas de la première simulation on a aussi
| la moyenne 16.0384 désintégrations en 50ms, l'écart
type est3.992 et la racine de16.0384 est 4.005= valeur théorique pour une distribution de POISSON dont la moyenne est 16.0384 |
 |
Etude de l'influence de la distance.
haut
Avec tracé de la courbe en fonction de la distance , avec régression
et ajustement linéaire.
Cette partie simule l'influence de la distance.
Les variables sont choisies avec les valeurs 5 pour " nombre de mesures" et 1000 pour "durée
de comptage" en milliseconde,
La distance est supposée fixée à 3cm.
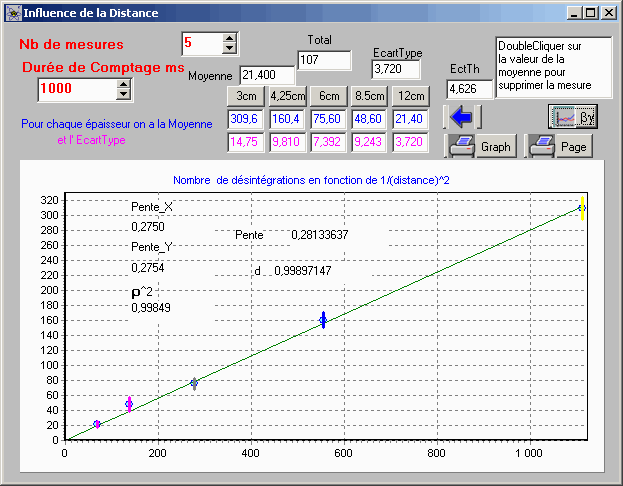
Note à propos des régressions :
Les valeurs des pentes des droites de régression affichées correspondent aux calculs suivants:
Pente_X
Les distances des points à la droite sont calculés en prenant les distances suivant la verticale
(X=constante)
Pente_Y
Les distances des points à la droite sont calculés en prenant les distances suivant l'horizontale
(Y=constante)
Pour l'ajustement linéaire,
la pente est calculée par ; (moyenne des produits x y )/(moyenne des x^2).
Etude de l'absorption des rayons par l'aluminium.
haut
Avec tracé des courbes Béta+ Gamma et Béta seul en fonction
de l'épaisseur , avec régression et ajustement linéaire.
Cette partie simule l'absorption des rayonnements par différentes épaisseurs d'aluminium.
Les variables sont choisies avec les valeurs 5 pour " nombre de mesures" et 10000 pour "durée
de comptage" en milliseconde soit 10s qui est une valeur expérimentale réaliste.
La distance est supposée fixée à 3cm.
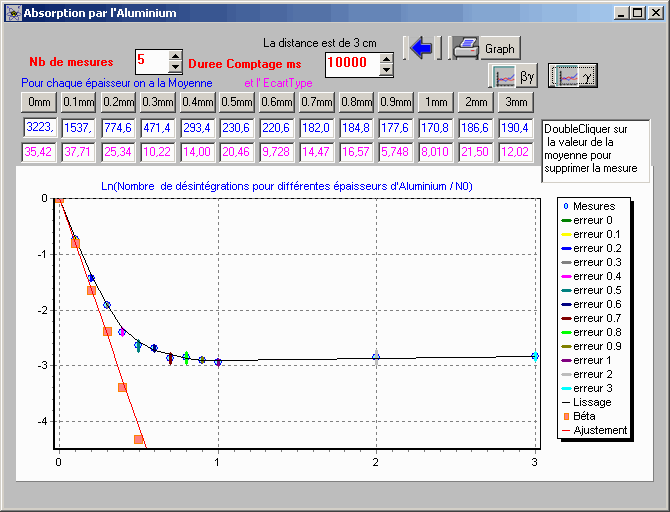
Etude de l'absorption des rayons par le plomb.
haut
Avec tracé de la courbe en fonction de l'épaisseur , avec régression
et ajustement linéaire.
Cette partie simule l'absorption des rayonnements par différentes épaisseurs de plomb, la première
mesure est effectuée avec un écran de 3mm d'aluminium pour arréter les rayons Bétas.
Les variables sont choisies avec les valeurs 5 pour " nombre de mesures" et 10000 pour "durée
de comptage" en milliseconde,
La distance est supposée fixée à 3cm.

haut
Outils
La calculatrice lance les calculs, la fléche gauche retourne au menu, l'imprimante
sert à imprimer.
Sur une figure, un clic droit sur un point donne les coordonnées du point
La définition d'un rectangle avec le clic droit donne un zoom de la zone définie.
 donne
donne